Modeling and Analyzing Configurable Software with Weighted Automata

M. Sc. Robert Müller

Many modern software systems must be highly configurable to suit diverse customer requirements. In this regard, software product-line engineering defines an approach for systematically developing a family of software variants. Features are user-configurable options that define the variable parts of a product line. Recent product-line engineering approaches are commonly restricted to finite Boolean configuration spaces, where a configuration is a subset of features. Furthermore, feature models are often used to concisely define the sub-space of valid configurations for a particular set of features.

Features are also used to map variability between the problem space and the solution space. Approaches commonly attach presence conditions (propositional formulae over features) to elements of the solution-space model. Thereby, presence conditions define how to extract the model for a particular variant from a configurable model that superimposes all variants. However, for modern systems like cloud-based software and industrial factories, Boolean variability is not sufficiently expressive, as customers can select features not only zero or one time but also multiple times and potentially even without upper bound. Hence, cardinality-based feature models have been devised as a generalization of Boolean feature models to support modeling the multiplicity of features. Cardinality-based feature models define the valid number of instances per feature as well as valid feature combinations. The number of feature instances can also be unbounded, resulting in infinite configuration spaces.

Applying feature-mapping techniques from Boolean feature models to cardinality-based feature models is challenging. Whereas structural modeling formalisms like UML often have integrated constructs for defining multi-instance model elements, typical behavioral models like transition systems do not have similar formalisms. With Boolean variability, the customer is faced with the choice of which feature to select or deselect. With multi-instance variability, the customer is faced with a more complex choice of selecting a specific number of instances of each feature. Selecting a maximum number of feature instances is not feasible, as this leads to excessive costs and is not applicable at all when features are unbounded. Therefore, we separately have to assess non-functional properties and the associated optimization objectives to pick optimal configurations.

We make use of weighted automata as a behavioral model to map configuration spaces of cardinality-based feature models to behavioral variability in the solution space. Weighted automata are a generalization of Boolean finite automata, that map accepted words to arbitrary weights instead of Booleans. The weights in a weighted automaton and the operations on them are defined by a semiring structure. We make use of multisets over the feature set as weights, to denote the required number of feature instances required to fire particular transitions. Thereby, we can establish a mapping between configurations of the cardinality-based feature model being represented as multisets and the behavior of a weighted automaton.

Based on the use of multisets to model variability, we extend the use of weighted automata to also represent non-functional properties of accepting runs. Hence, we represent both variability as well as optimization objectives using weights. To find optimal configurations regarding a specific objective we can perform a shortest-path search considering that objective on the weighted automaton. To find optimal configurations regarding multiple objectives, we make use of the weighted-sum method to optimize multiple conflicting objectives.

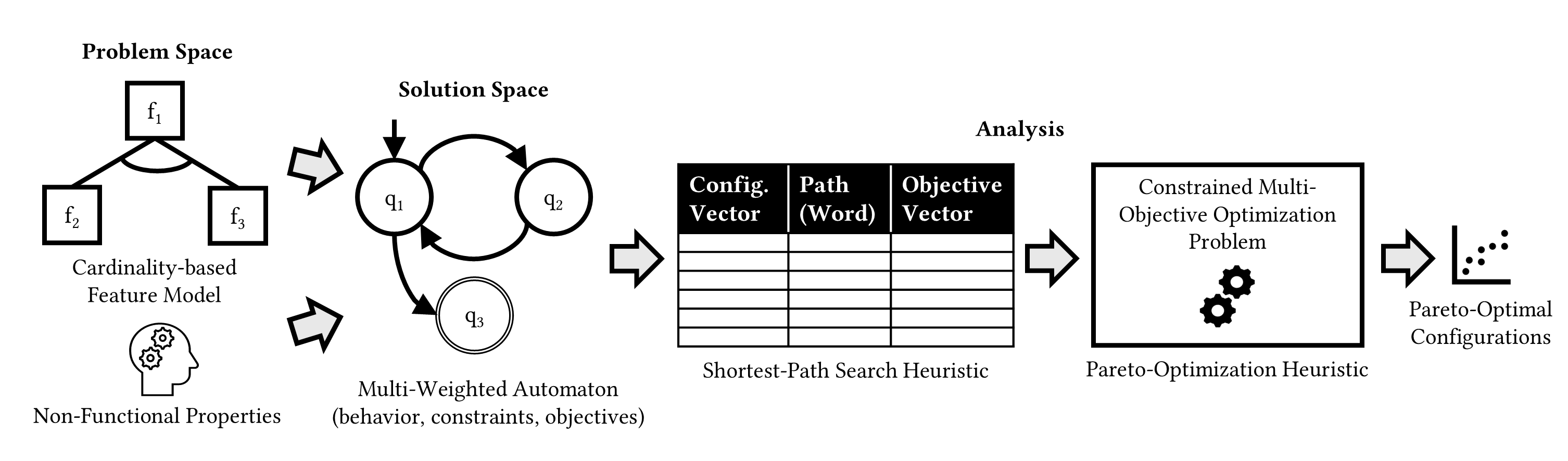
The figure below shows an overview of our analysis pipeline. In the problem space, we use a cardinality-based feature model to specify the valid configuration space using multi-instance features and we require knowledge of the non-functional properties as input. In the solution space, we encode the behavior of the system using a multi-weighted automaton. The different weights in the automaton allow us to model constraints of individual system actions as well as the impact of actions on non-functional properties. This allows us to find optimal configurations by using analysis techniques for weighted automata. To this end, we perform several shortest-path searches on the weighted automaton with different relative weightings of the objective values. Finally, we perform Pareto analysis on the combined shortest-path results to obtain a set of Pareto-optimal configurations for the system.

Robert Müller, Mathis Weiß, and Malte Lochau. „Finding Optimal Configurations of Cardinality-based Feature Models using Weighted Automata.“ Proceedings of the 29th ACM International Systems and Software Product Line Conference – Volume A (SPLC-A ’25). 2025. [ACM Digital Library]

Robert Müller, Mathis Weiß, and Malte Lochau. „Mapping Cardinality-based Feature Models to Weighted Automata over Featured Multiset Semirings.“ Proceedings of the 28th ACM International Systems and Software Product Line Conference. 2024. [Definitive Version] [Extended Version]

Part of DFG Project Co-InCyTe (LO 2198/4-1).